Materials

Here, I will walk through the concepts behind creating a material system. This is a system whose goal is to represent standard material appearances on surfaces, using parameters that the developer (or artist) can tweak.

BSDFs and BRDFs §

The BSDF §

Mathematically, a material model is described by a Bidirectional Scattering Distribution Function (BSDF). The BSDF a function that describes how light scatters upon interacting with a surface.

Given an incident light angle and an outgoing angle, this function returns how much of the light is scattered into the outgoing direction.

The BSDF itself is composed of two other functions:

• The Bidirectional Reflectance Distribution Function (BRDF): Describes how light scatters off of the surface.
• The Bidirectional Transmittance Distribution Function (BRTF): Describes how light transmits through the surface.

BSDF

In our case, we will focus on creating a physically based BRDF, and ignore the BRTF (which can be quite complex to model).

The BRDF §

The BRDF is a function that describes how a surface material responds to light. It is made up of two terms:

• A diffuse component, denoted $f_d$
• A specular component, denoted $f_s$

Let $v$ be a unit vector from the surface to our view, and $l$ be a unit vector from the light to our surface. Then, our BRDF is given as the sum of the diffuse and specular components.

$$f(v,l)=f_d(v,l)+f_r(v,l)$$

Using this function, if we fix our view $v$ and evaluate this function over all possible light directions $l$, we can accumulate the final color value that we see.

$$c=\int f(v,l)dl$$

By allowing $f_d$ and $f_r$ to vary with different parameters, we can model a wide variety of different materials.

One of the common models for this is known as the Metallic-Roughness Model, which we’ll describe next.

The Metallic-Roughness BRDF §

The Metallic-Roughness BRDF is a BRDF that has two toggleable parameters: metallic and roughness.

Metallicness (Dielectrics vs. Conductors) §

Metallicness defines how metallic a material is. To understand why this affects the resulting look, it’s important to understand how the diffuse and specular components, $f_d$ and $f_r$, occur in reality.

• The specular component, $f_r$, occurs due to light reflecting directly off of the surface.
• The diffuse component, $f_d$, occurs due to subsurface scattering: how light penetrates and scatters inside the surface.

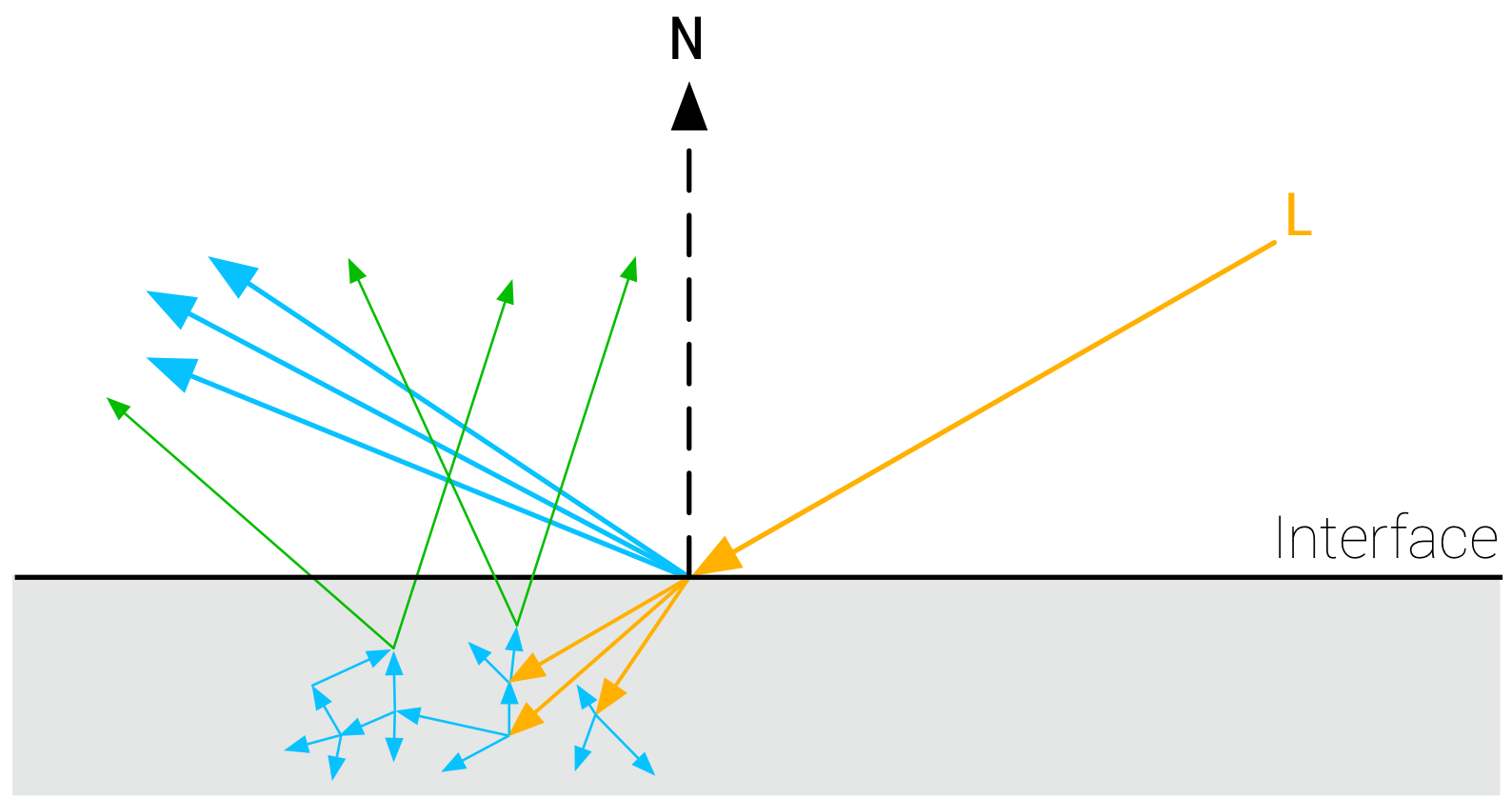
A visual depiction of subsurface scattering. Our diffuse component in fact is an approximation of this subsurface scattering.

Subsurface scattering explains the difference between metal and non-metal materials. Subsurface scattering does not occur in pure metals, meaning metals do not have a diffuse component. This affects the perceived resulting color.

Roughness (Microfacets) §

Roughness defines the degree of irregularity a surface has.

In a basic BRDF, it’s assumed that the surface is perfectly flat. However, in reality, surfaces always have some degree of irregularity, with small randomly aligned fragments (microfacets) that create apparent “roughness”.

• Left: A more physically plausible surface with microfacets
• Right: An unrealistic perfectly flat surface

These microfacets change a surface’s appearance, due to interactions between them that occur on a micro scale.

• Not all microfacets will reflect light towards the camera.
  • Light may not reach some microfacets, as it will be blocked (shadowed) by another microfacet.
  • Even if light reaches a microfacet, it may not reach the camera, as it may still be blocked (masked) by another microfacet.

Because of this, the degree of alignment between microfacets determines how much light is reflected towards the camera. This in turn influences the perceived roughness of our surfae.

• Smoother surfaces have more microfacets that are aligned, and thus reflect more light towards the camera
• Rougher surfaces have less microfacets that are aligned, and thus reflect less light towards the camera

The BRDF Model §

With these more physically-plausible assumptions, our BRDF is now defined as follows (for both the specular / diffuse components). Let $\alpha$ be the roughness of our material.

$$f_x(v,l)=\frac{1}{|n\cdot v||n\cdot l|}{\int }_{\Omega }D(m,\alpha ),G(v,l,m)f_m(v,l,m)(v\cdot m)(l\cdot m)dm$$

Where:

• $D(m,\alpha )$ is known as the Normal Distribution Function (NDF) and models the distribution of the microfacets
• $G(v,l,m)$ models the visibility of the microfacets that occurs due to shadowing or masking
• $f_m$ is the diffuse / specular function

The final lighting value requires us integrate over the entire hemisphere, and as this is not practical, we will rely on approximations for this equation for both the specular and diffuse components (coming next).

Energy Conversation

A good physically-based BRDF is one that will conserve energy. In other words, it guarantees that the total amount of specular / diffuse energy is always less than the total amount of incident energy. We can’t just create energy out of nothing!

Metallic-Roughness BRDF Implementation §

Here, we describe an implementation of the metallic-roughness BRDF, split between the specular and diffuse components.

Specular BRDF §

The specular $f_r$ can be modeled as follows. This is called the Cook-Torrance approximation of the previously seen integration. Let $h$ be the half unit vector between $l$ and $v$.

$$f_r(v,l)=\frac{D(h,\alpha ),G(v,l,\alpha ),F(v,h,f_0)}{4(n\cdot v)(n\cdot l)}$$

Where:

• $D(h,\alpha )$ models the distribution of the microfacets
• $G(v,l,\alpha )$ models the occlusion of the microfacets
• $F(v,h,f_0)$ accounts for Fresnel’s law, modeling the fact that the amount of reflected light on a surface depends on the viewing angle

Refer to https://graphicrants.blogspot.com/2013/08/specular-brdf-reference.html for many formulations of these 3 terms.

…

Normal Distribution Function (D) §

References §

• https://google.github.io/filament/Filament.html#materialsystem